In hypothesis testing, the z-score table plays a significant role. It helps statisticians and researchers determine the probability of certain values occurring in a standard normal distribution. By using this table, they can make informed decisions about their hypotheses and draw conclusions based on their findings.
The Z-Score Table
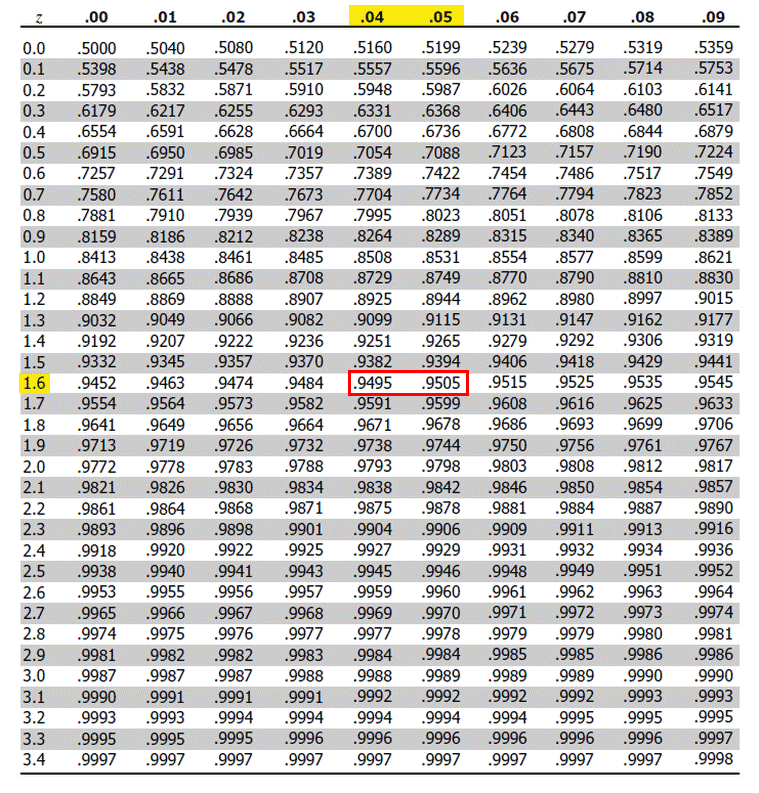The z-score table, also known as the standard normal distribution table, provides critical values for the standard normal distribution. These critical values correspond to specific probabilities or areas under the curve.
How to Use the Z-Score Table
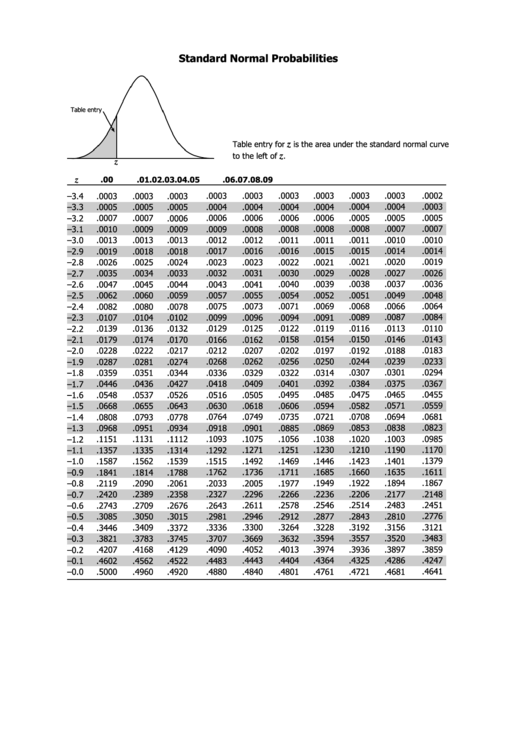To use the z-score table, we need to follow a few simple steps:
1. Start by finding the z-score of the value you are interested in. The z-score measures the number of standard deviations a particular value is from the mean. It allows us to standardize values and compare them to the standard normal distribution.
2. Once you have the z-score, locate the corresponding row and column in the z-score table. The rows represent the whole number part of the z-score, while the columns represent the decimal part. The intersection of the row and column will give you the area or probability associated with that z-score.
3. Now you can interpret the area or probability you found in the z-score table. It represents the likelihood of obtaining a value equal to or less than the z-score. You can use this information to make decisions or draw conclusions about your hypothesis.
Importance of the Z-Table
For example, let’s say a researcher wants to test the hypothesis that the average test score of a particular group of students is significantly different from the general population. By calculating the z-score for the sample mean and referring to the z-table, the researcher can determine the probability of obtaining a score as extreme or more extreme than the observed value. This probability helps in accepting or rejecting the null hypothesis.
Moreover, the z-table is widely used in statistical analysis, especially in areas like quality control, research studies, and financial modeling. It allows analysts to determine the likelihood of certain events occurring and make data-driven decisions based on statistical probabilities.
Limitations and Alternatives
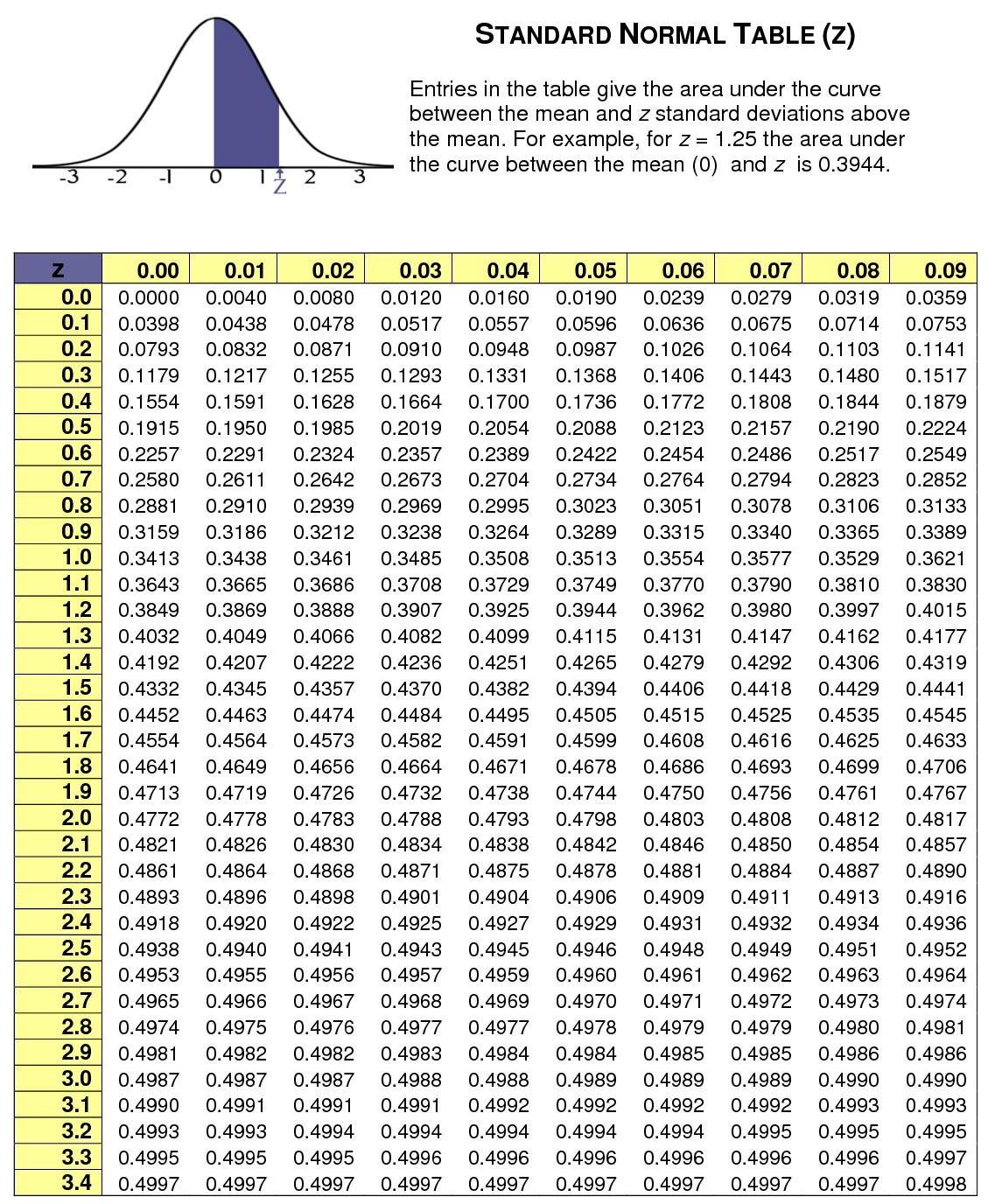While the z-table is a valuable tool, it does have a few limitations. Firstly, it only provides probabilities for values below the mean. To determine the probability of values above the mean, one must use complementary probabilities (1 - probability). Additionally, the z-table assumes a standard normal distribution, meaning that the data must be normally distributed.
In cases where the data does not meet the assumptions of the standard normal distribution, alternate methods like non-parametric tests or transformation techniques may be employed. These alternatives provide more flexibility and allow for hypothesis testing in a wider range of scenarios.
Conclusion
The z-score table is a fundamental tool in hypothesis testing and statistical analysis. It enables researchers to determine the probability of specific values occurring in a standard normal distribution. By understanding how to use the z-table, statisticians can make informed decisions, draw conclusions about their hypotheses, and evaluate the significance of their findings. However, it is essential to acknowledge the limitations of the z-table and consider alternative methods when the data does not meet the assumptions of a standard normal distribution. Through the proper use of the z-table and other statistical tools, researchers can gain valuable insights from their data and contribute to the field of statistics.
